Gyori’s Proof
Claim
[n/4] guards are sometimes necessary, but always sufficient to guard the interior of an n-wall orthogonal art gallery.
A Stronger Claim
We will instead prove a stronger claim than the one above, that:
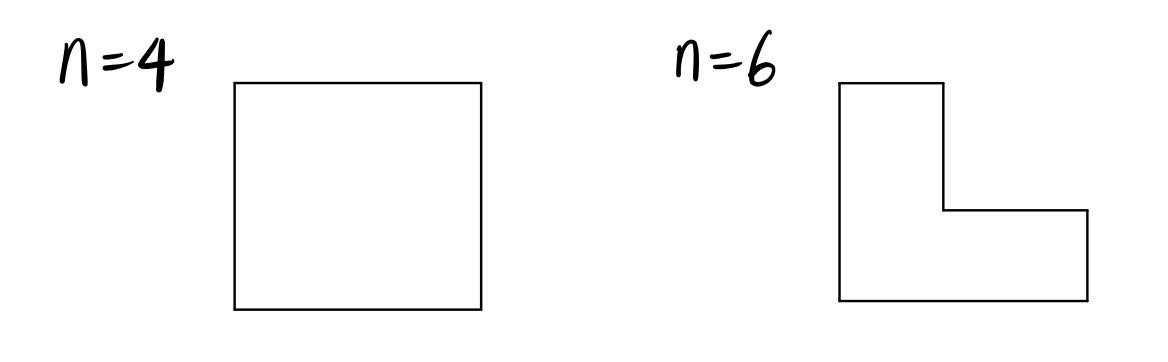
if P is an orthogonal polygon of n vertices, then P can be partitioned into at most [n/4] orthogonal polygons of 4 or 6 vertices.
To see why this implies the previous claim, we can see that orthogonal polygons of 4 or 6 vertices are of unique shapes, being rectangular or in the shape of a capital letter “L” respectively. It is easy to see that one guard is sufficient to guard each.
Some Facts about P(Orthogonal Polygon)
- The internal angles of P are of 90 degrees (convex) or 270 degrees (concave).
- The sides of P are alternately horizontal and vertical, which means n must be even.
- For P, the number of concave vertices is 4 less than the number of convex vertices.
Base Case of An Inductive Proof
If n is 4 or 6, we have nothing to prove (base case). Since n must be even, let’s assume that n >= 8.
Case 1 (Easy)
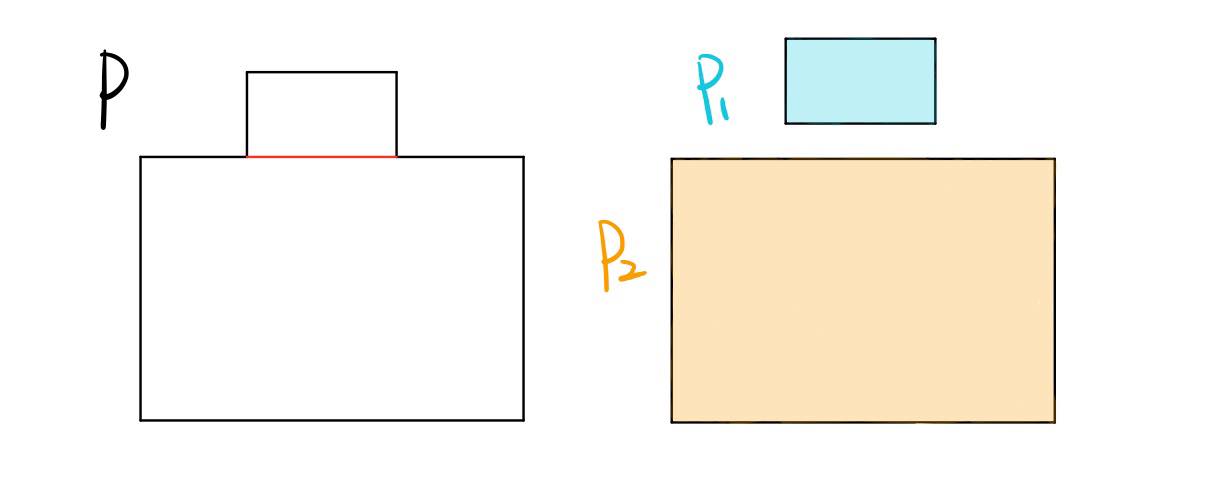
There are two vertices of P that can be connected by a horizontal or vertical segment without crossing the boundary of P. If this is the case, we can cut P along that very segment and we will obtain 2 new polygons P1 and P2 of n1 and n2 vertices, respectively, such that n1 + n2 = n. We are done by inductive hypothesis.
Case 2 (Easy)
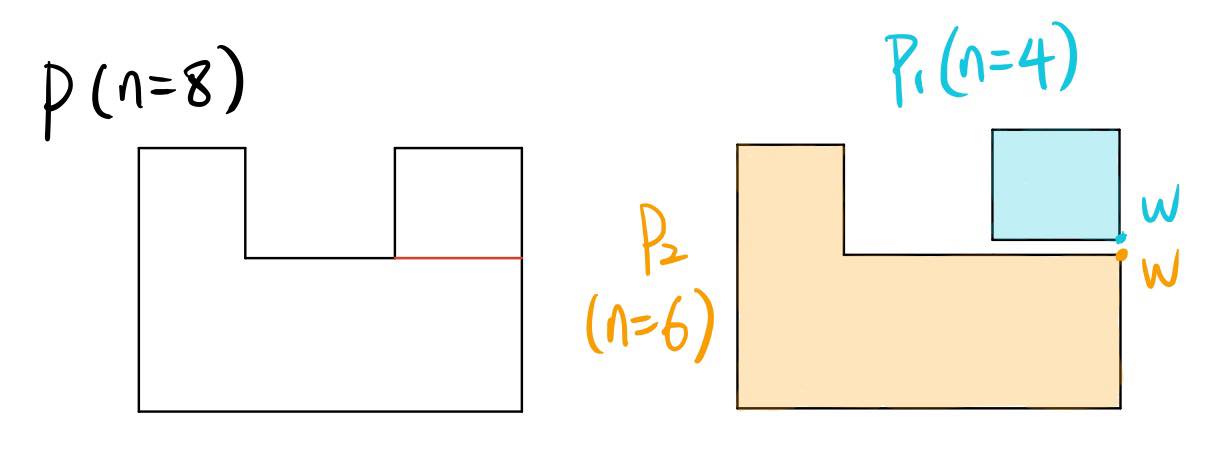
This is the case where n = 4k, where k is some integer > 1. If we take a concave vertex V of the polygon P and cut P horizontally through the boundary of P, we will obtain 2 new polygons P1 and P2 of n1 and n2 vertices, respectively, such that n1 + n2 = n+2. It is becasue the cut creates a new vertex, W, which is used by both P1 and P2. We are done by inductive hypothesis because:
n1/4 + n2/4 <= (n+2)/4 = n/4
Case 3 (Hard)
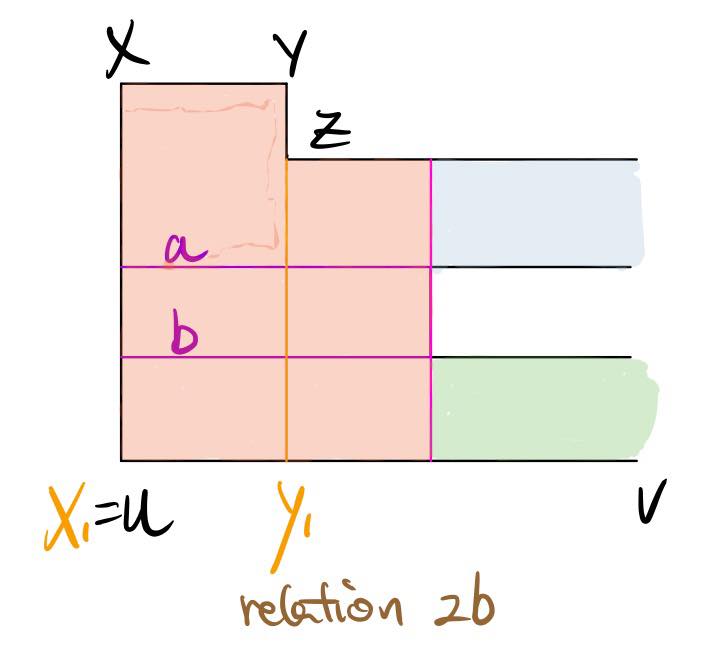
We are left with the case where n = 4k+2, where k is some integer > 1. According to the fact 3, P must have 2k+3 convex vertice and 2k-1 concave vertice. Therefore, there exist two neighboring convex vertice in P which we can call X and Y. If we move the side XY orthogonally through the interior of P as far as P’s boundary, let X1 and Y1 denote the images of X and Y, respectively, under the translation.
Suppose that upon our cutting the rectangle XYX1Y1 out of P, we should obtain either 1 or 2 polygons. The only scenario whereupon our cutting we will obtain more than 2 polygons is shown below. However, in this scenario, a horizontal segment can be connected between A and B without crossing the boundary of P, which means it is in Case 1. Because we are in Case 3, we cannot find such A and B. As proved by contradiction, we will obtain either 1 or 2 polygons upon cutting the rectangle XYX1Y1.
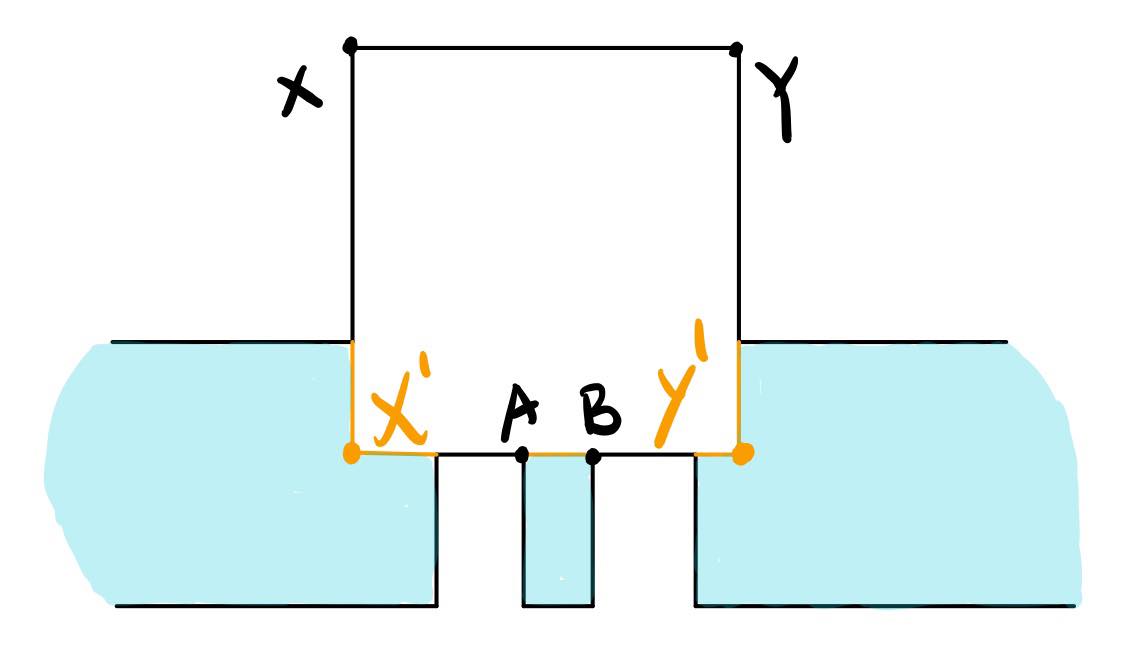
Scenario I: 2 Polygons
In the case where we obtain 2 polygons upon cutting the rectangle XYX1Y1, X1Y1 only intersects with one side UV of P. There are 3 different relations between the side UV and the segment X1Y1.
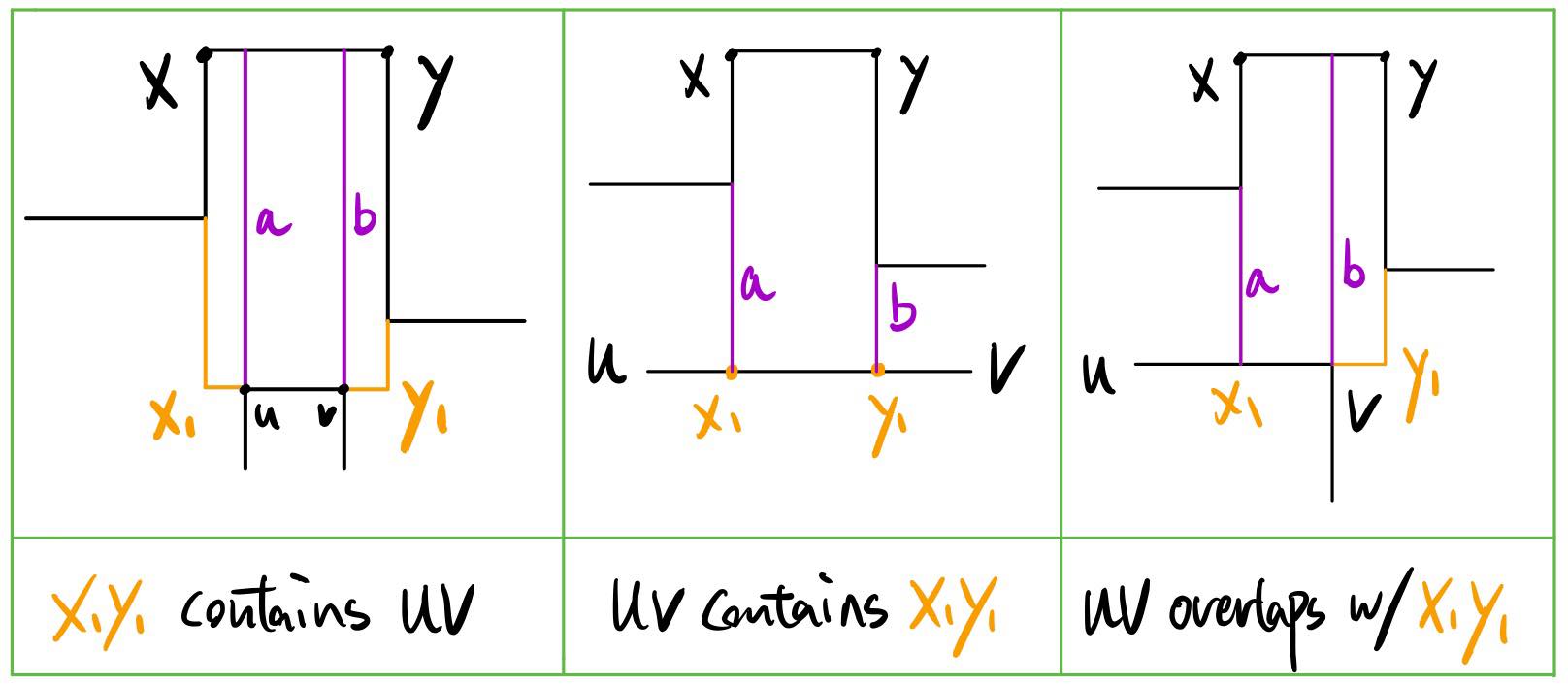
In each relation above, we may cut P along the purple segment a or b. One of the cut will yield 2 new polygons P1 and P2 of n1 and n2 vertice, respectively, such that n1 = 4k1 + 2, n2 = 4k2 + 2, and k = k1 + k2. Therefore we are done by the inductive hypothesis.
Here are 3 examples, one for each relation:
Example 1: X1Y1 contains UV
Example 2: UV contains X1Y1
Example 3: UV overlaps with X1Y1
Scenario II: 1 Polygons
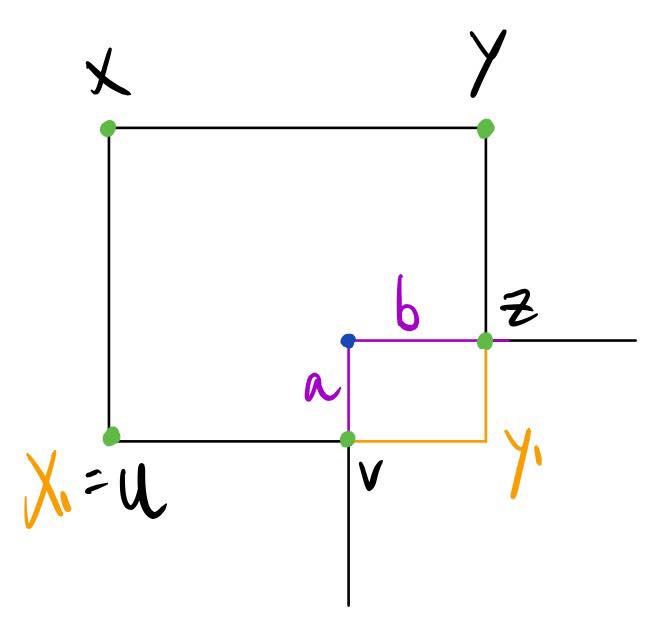
In the case where we obtain only 1 polygon upon cutting the rectangle XYX1Y1, XX1 or YY1 must be a side of P. Here we assume that XX1 is a side of P and X1 = U.
There are 2 relations:
Relation 1: When X1Y1 contains the side X1V and YY1 contains the side YZ of P, we cut P along the segments a and b obtaining P1 (the L-shaped one) of 6 vertice and P2 (the rest) of 4k-2 vertice. It is easy to see why P2 must have 4k-2 vertice: the cutting reduces 5 green vertice from it and adds 1 vertex to it. Therefore, 4k+2-5+1 = 4k-2. 4k-2 = 4(k-1) + 2. We are done by inductive hypothesis.
Relation 2a: When X1Y1 is contained in the side X1V and YY1 contains the side YZ of P, we cut off a L shaped polygon by cutting vertically along the segment a. The remaining must be of 4k-2 vertice. The reasoning is exactly the same as the relation 1.
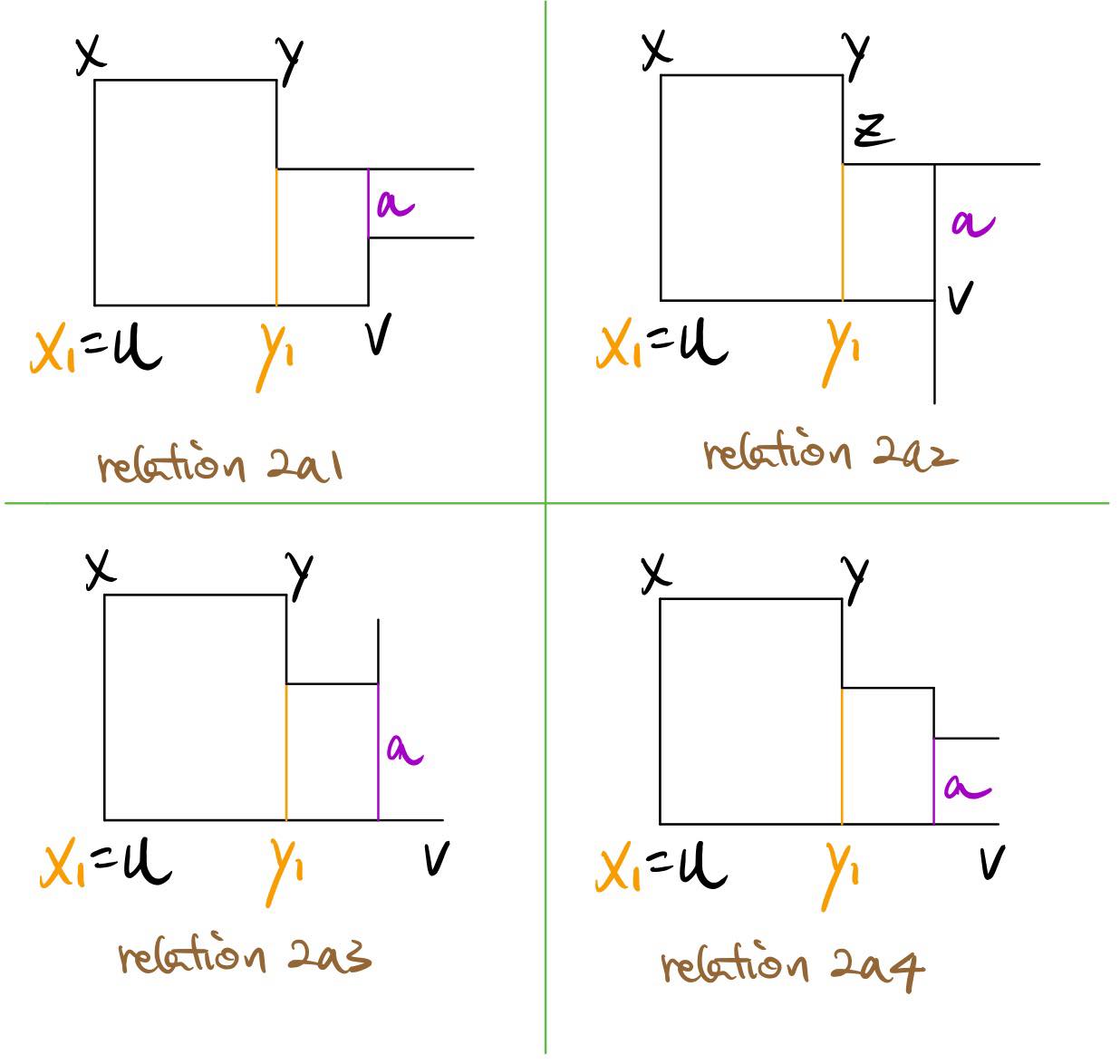
Therefore, we are done by inductive hypothesis unless the cut slices P into 3 or more pieces.
Relation 2b: As shown in the figure below, if we were to cut vertically along the pink line like we used to do for relation 2a, we would slice the polygon P into 3 pieces (the red, the grey, and the green). Therefore, we would need to perform a horizontal cut either along segment a or along segment b. One of these 2 possible cuts will cut P into polygons P1 and P2 of 4k+2 and 4k+2 vertice, and k1 + k2 = k.
The reason is really similar, if not the same as, the reasoning of Case 3: Scenario 1.
Therefore, we are done by inductive hypothesis.