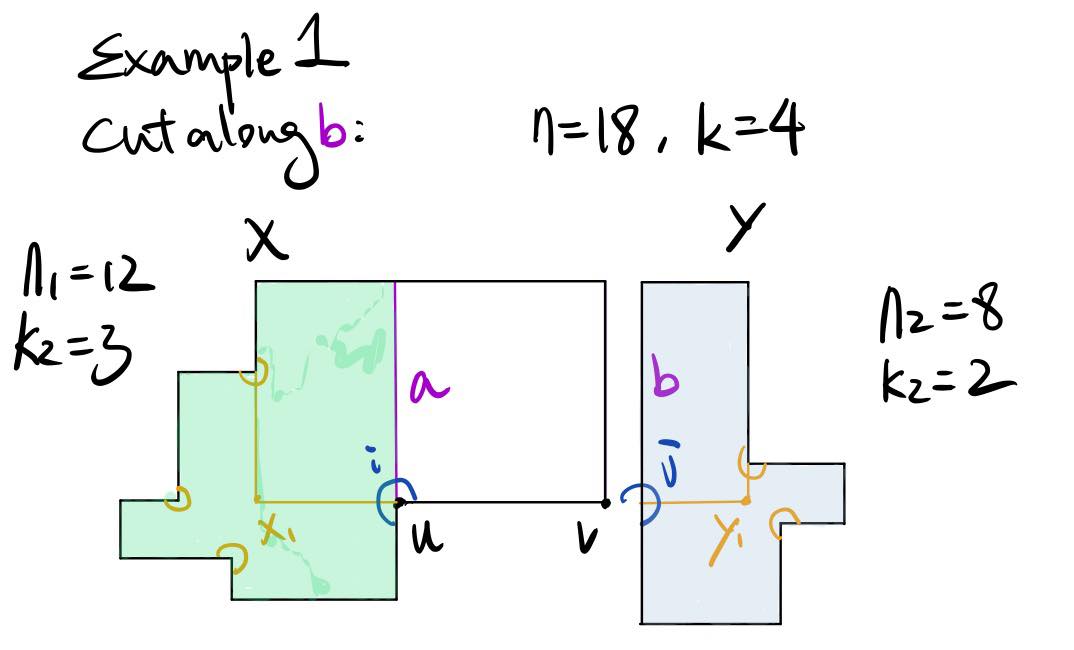
Example 1: X1Y1 contains UV
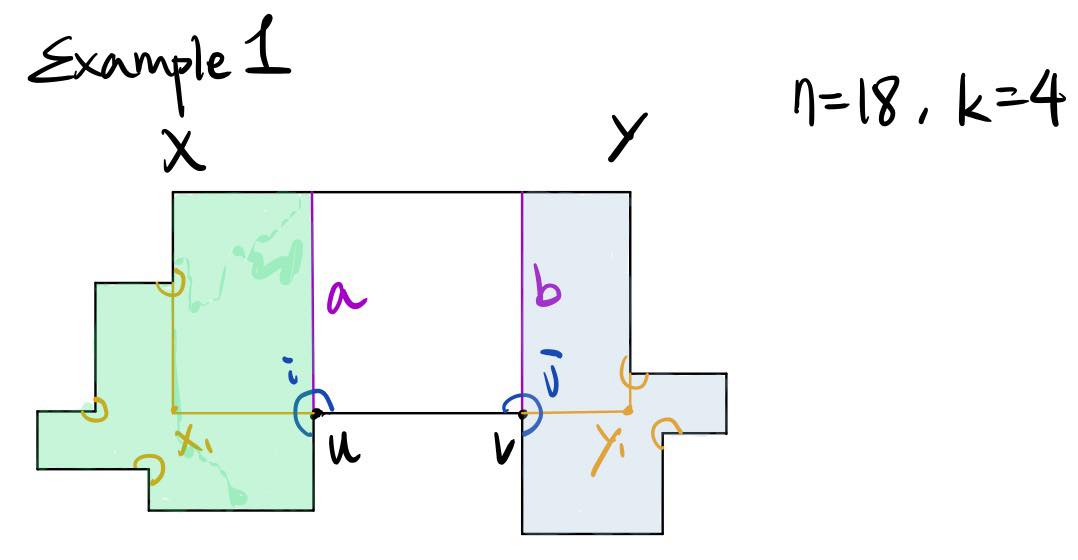
Example 1 covers the relation where X1Y1 contains UV, where n = 18 and k = 4. As established earlier, P must have 2k-1 concave vertices. Suppose that concave vertices i and j are now blocked by the segment a and b, the green polygon and grey polygon should have in total 2k-3 concave vertices. Because 2k-3 is odd, it implies that either the green polygon or the purple polygon has an even number of concave vertices. If we cut along segment a, j will be freed to join the grey polygon. Similarly, if we cut along segment b, i will be freed to join the green polygon. Therefore, if the green polygon has an even number of concave vertices, we should cut along segment b; if the grey polygon has an even number of concave vertices, we should cut along segment a.
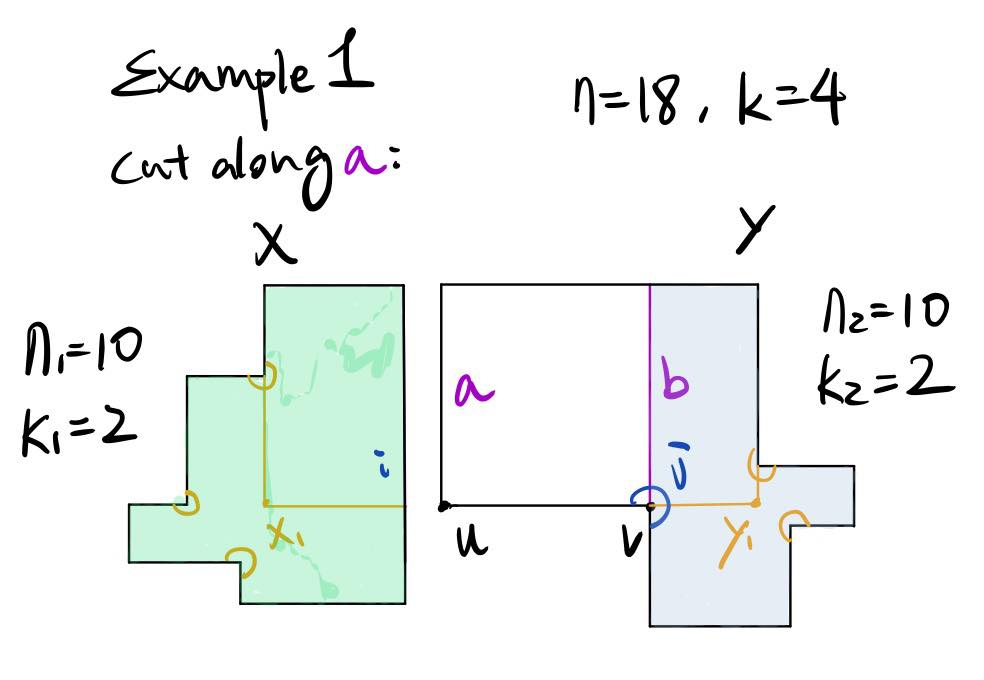
Here the grey polygon has an even number of concave vertices, which suggests that we should cut along segment a. After performing such cut, we will find that n11 = 10, k1=2, n2=10, k2=2, which means n1 = 4k1 + 2, n2 = 4k2 + 2. We also find that after the cut, 2 new vertices are produced: 4k1 + 2 + 4k2 + 2 = 4k + 2 + 2 k1 + k2 = k
If we cut along segment b, k1 + k2 > k. Therefore, the inductive hypothesis won’t work.