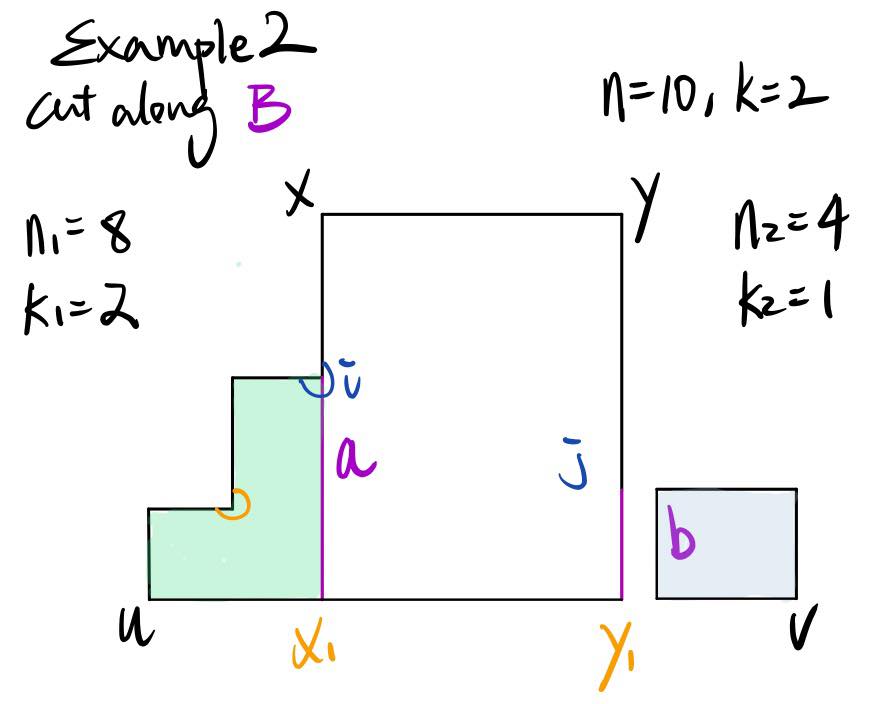
Example 2: UV contains X1Y1
Example 2 covers the relation where UV contains X1Y1, where n = 10 and k = 2. As established earlier, P must have 2k-1 concave vertices. Suppose that concave vertices i and j are now blocked by the segment a and b, the green polygon and grey polygon should have in total 2k-3 concave vertices. Because 2k-3 is odd, it implies that either the green polygon or the purple polygon has an even number of concave vertices. If we cut along segment a, j will be freed to join the grey polygon. Similarly, if we cut along segment b, i will be freed to join the green polygon. Therefore, if the green polygon has an even number of concave vertices, we should cut along segment b; if the grey polygon has an even number of concave vertices, we should cut along segment a.
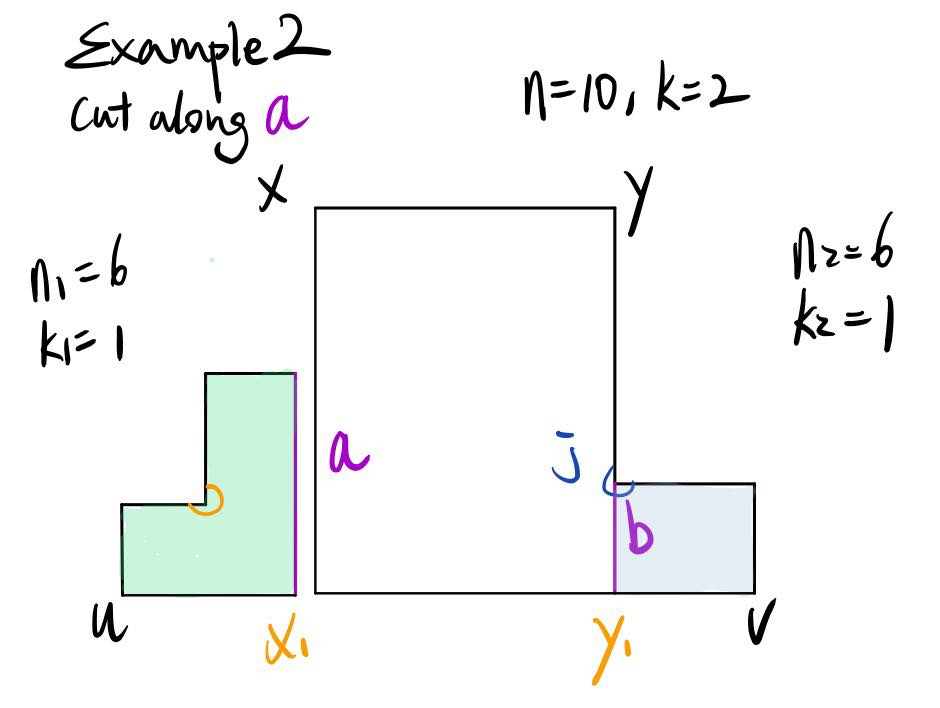
Here the grey polygon has 0 concave vertex (even), which suggests that we should cut along segment a. After performing such cut, we will find that n11 = 6, k1=1, n2=6, k2=1, which means n1 = 4k1 + 2, n2 = 4k2 + 2. We also find that after the cut, 2 new vertices are produced: 4k1 + 2 + 4k2 + 2 = 4k + 2 + 2 k1 + k2 = k
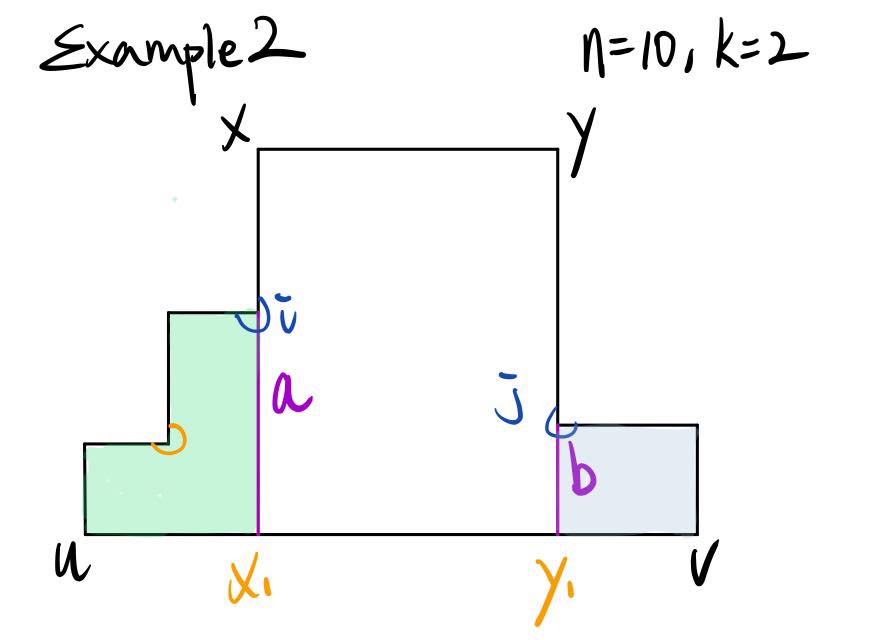
If we cut along segment b, k1 + k2 > k. Therefore, the inductive hypothesis won’t work.